백준 2086번 피보나치 수의 합 - C++ 풀이

---

 

1. 1번째 항부터 n번째 항까지의 합을 g(n)이라 하면, g(n) = g(n-1) + g(n-2) + 1
2. 점화식을 행렬 곱으로 나타낸다.
3. 분할 정복을 이용하여 행렬의 거듭제곱을 계산한다.

 

1. 1번째 항부터 n번째 항까지의 합을 g(n)이라 하면, g(n) = g(n-1) + g(n-2) + 1

 피보나치수열을 점화식으로 나타내면 f(n) = f(n-1) + f(n-2), f(1) ~ f(n)의 합을 g(n)이라고 하면, g(n) = g(n-1) + g(n-2) + 1이다.

 

2. 점화식을 행렬 곱으로 나타낸다.

 g에 대한 점화식을 다음과 같은 행렬 곱으로 나타낼 수 있다.

 

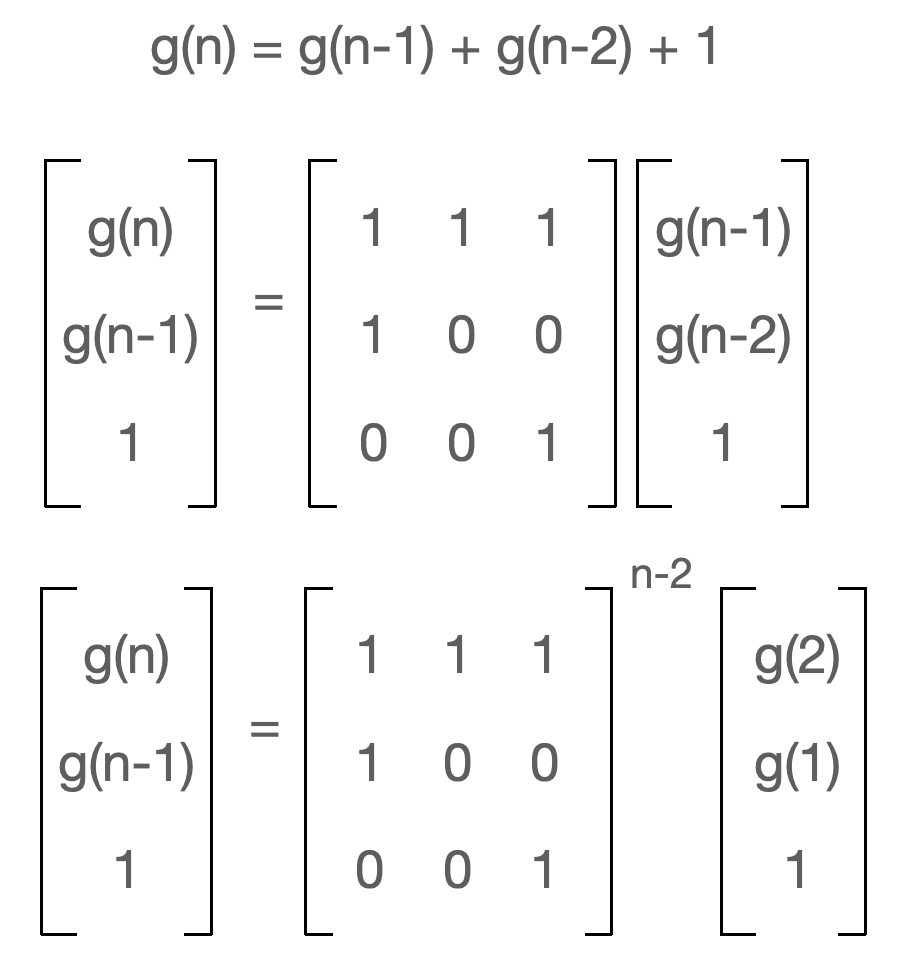
3. 분할 정복을 이용하여 행렬의 거듭제곱을 계산한다.

 분할 정복을 이용하여 거듭제곱을 계산하여 시간 초과를 피한다.

반응형

---

#include <iostream>
#include <vector>

using namespace std;

typedef long long ll;
typedef vector<vector<ll>> Matrix;
const ll MOD = 1000000000;

ll A, B;
vector<vector<ll>> matrix =
{
    {1, 1, 1},
    {1, 0, 0},
    {0, 0, 1}
};

Matrix matrixMultiply(Matrix x, Matrix y) {
    int R = x.size(), C = y[0].size();
    Matrix ret = vector<vector<ll>>(R, vector<ll>(C, 0));
    
    for (int i=0; i<R; i++) {
        for (int j=0; j<C; j++) {
            for (int k=0; k<y.size(); k++) {
                ret[i][j] += (x[i][k] * y[k][j]) % MOD;
                ret[i][j] %= MOD;
            }
        }
    }
    
    return ret;
}

Matrix matrixPower(ll n) {
    if (n == 1) return matrix;
    
    Matrix half = matrixPower(n/2);
    if (n % 2 == 0) return matrixMultiply(half, half);
    else return matrixMultiply(matrix, matrixMultiply(half, half));
}

ll psum(ll n) {
    if (n <= 2) return n;
    
    Matrix res = matrixPower(n-2);
    return (2*res[0][0] + res[0][1] + res[0][2]) % MOD;
}

int main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(NULL); cout.tie(NULL);
    
    cin >> A >> B;
    cout << (psum(B) - psum(A-1) + MOD) % MOD;
}