1. 오른쪽부터 왼쪽으로 가면서 오큰수를 구할 것이다.
2. 스택에는 앞으로 오큰수가 될 수 있는 수들만 들어있게 유지한다.
3. 어떤 수 x를 고려하는 시점에서의 스택 top이 x의 오큰수이다.
1. 오른쪽부터 왼쪽으로 가면서 오큰수를 구할 것이다.
오른쪽부터 왼쪽으로 가면서 오큰수를 구할 것이다. 즉 NGE(N), NGE(N-1), ..., NGE(2), NGE(1) 순으로 구할 것이다.
2. 스택에는 앞으로 오큰수가 될 수 있는 수들만 들어있게 유지한다.
스택을 사용한다. 스택에는 앞으로 어떤 수의 오큰수가 될 수 있는 수들만 들어있게 유지해준다. 주어진 수열을 높이가 있는 막대라고 생각해보자.

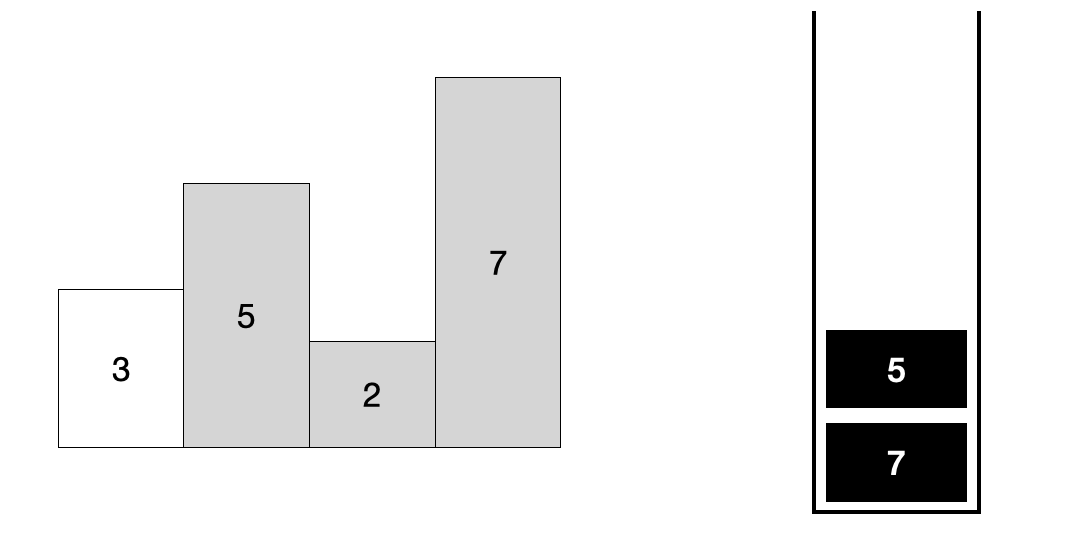
먼저 가장 오른쪽에 있는 7의 오큰수인 NGE(4)를 구해보자. 스택이 비어있으므로 7의 오큰수는 없다. 만약 스택이 비어있다면 오큰수가 없는 것이다.

하지만 7은 왼쪽에 있는 수들의 오큰수가 될 가능성이 있다. 왼쪽에 7보다 더 작은 수가 나오면 7이 그 수의 오큰수가 되기 때문이다. 따라서 7을 스택에 푸시해준다. 앞으로 모든 수는 더 왼쪽에 나오는 수의 오큰수가 될 확률이 있으므로 스택에 푸시해준다.

이제 2의 오큰수인 NGE(3)을 구해보자. 스택에 7이 들어있고, 2보다 7이 크고 2의 오른쪽에 등장하므로 7은 2의 오큰수이다.

또한 2도 더 왼쪽에 오는 수의 오큰수가 될 수도 있으므로 스택에 푸시해준다.

이제 5의 오큰수인 NGE(2)를 구해보자. 스택에 2와 7이 들어있다. 먼저 2는 5보다 작으므로 5의 오큰수가 될 수 없다. 그리고 이제 2는 어떤 수의 오큰수가 될 가능성이 없어졌다. 2의 왼쪽에 2보다 큰 5가 등장했기 때문이다. 5가 2를 가리고 있기 때문에 절대 2는 왼쪽에 있는 수의 오큰수가 될 수 없다. 따라서 2를 팝 해준다.
이렇게 스택에 현재 고려하고 있는 수보다 작은 수가 있다면 전부 팝 해서 스택 내부에는 현재 수보다 큰 수만 있도록 만들어준다.

이제 스택에 담긴 7을 보자. 7은 5보다 크고 오른쪽에 있으므로 7은 5의 오큰수이다.

또 5도 왼쪽에 나오는 어떤 수의 오큰수가 될 수 있으므로 푸시해준다.

3. 어떤 수 x를 고려하는 시점에서의 스택 top이 x의 오큰수이다.
마지막으로 3의 오큰수인 NGE(1)을 구해보자. 현재 스택에는 5와 7이 들어있다. 두 수 모두 3보다 크기 때문에 3의 오큰수가 될 수 있다. 둘 중에 3의 오큰수는 더 3과 가까이에 있는 수가 되어야 한다. 따라서 더 나중에 스택에 들어간 수(스택 top)가 오큰수가 된다.
#include <iostream>
#include <stack>
using namespace std;
int N;
int arr[1000001];
int NGE[1000001];
stack<int> s;
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
cin >> N;
for(int i=1; i<=N; i++) {
cin >> arr[i];
}
for(int i=N; i>=1; i--) {
while (!s.empty() && s.top() <= arr[i]) s.pop();
if (s.empty()) {
NGE[i] = -1;
}
else {
NGE[i] = s.top();
}
s.push(arr[i]);
}
for(int i=1; i<=N; i++) {
cout << NGE[i] << " ";
}
return 0;
}
'Problem Solving > BOJ' 카테고리의 다른 글
| 백준 19587번 객실 배치 - C++(cpp) 풀이 (0) | 2022.02.23 |
|---|---|
| 백준 16637번 괄호 추가하기 - C++(cpp) 풀이 + 그림 설명 (0) | 2022.02.18 |
| 백준 3055번 탈출 - C++(cpp) 풀이 (0) | 2022.02.17 |
| 백준 2580번 스도쿠 - C++(cpp) 풀이 (0) | 2022.02.16 |
| 백준 11505번 구간 곱 구하기 - C++(cpp) 풀이 (0) | 2022.02.16 |




댓글