1. DFS를 돌면서 이어져있는 칸들을 Union한다. 각 집합마다 SAFE ZONE은 한 개만 있으면 된다.
2. 이미 방문한 점이더라도 Union은 하고 넘어간다.
3. 집합의 개수가 곧 SAFE ZONE의 개수이다.
1. DFS를 돌면서 이어져있는 칸들을 Union한다. 각 집합마다 SAFE ZONE은 한 개만 있으면 된다.
어떤 칸들이 하나의 경로로 이어져있다면 결국 경로 중 어느 칸에서 출발하더라도 계속 가다 보면 그 경로의 끝 칸에 도달하게 된다. 따라서 그 끝 칸에만 SAFE ZONE을 설치하면 된다. 한 경로로 이어져 있는 칸들을 하나의 집합으로 처리하기 위해 유니온 파인드를 사용한다. DFS를 돌면서 한 경로로 이어져있는 칸들을 모두 union 해준다.
2. 이미 방문한 점이더라도 Union은 하고 넘어간다.
DFS를 돌 때 유의할 점이 있다. 다음 칸이 이미 방문한 칸이라면 DFS를 돌진 않아도 Union은 해주고 넘어가야 한다. 아래와 같은 상황이 그 예이다. (0,0)에서 DFS를 시작해서 union 작업을 하면

아래에 빨간색으로 표시된 칸들을 방문하고 한 집합으로 union할 것이다. 여기서 (1,3)에서 DFS를 시작하면,

회색 칸이 이미 방문된 칸이므로 (2,2) 방문을 마지막으로 DFS를 종료하게 된다.

그런데 자세히 살펴보면 아래 두 회색칸 중 하나만 SAFE ZONE이면 모든 빨간색과 초록색 칸에서 해당 SAFE ZONE에 도달이 가능하다는 것을 알 수 있다. 두 개의 경로(빨간색과 초록색)의 끝이 동일하다는 의미이다. 각 경로의 끝에만 SAFE ZONE을 설치해주기로 했는데, 두 경로의 끝이 같으므로 SAFE ZONE을 하나로 공유할 수 있게 되었다. 따라서 두 경로를 union 해주고 넘어가야 "최소" 개수를 구할 수 있다.

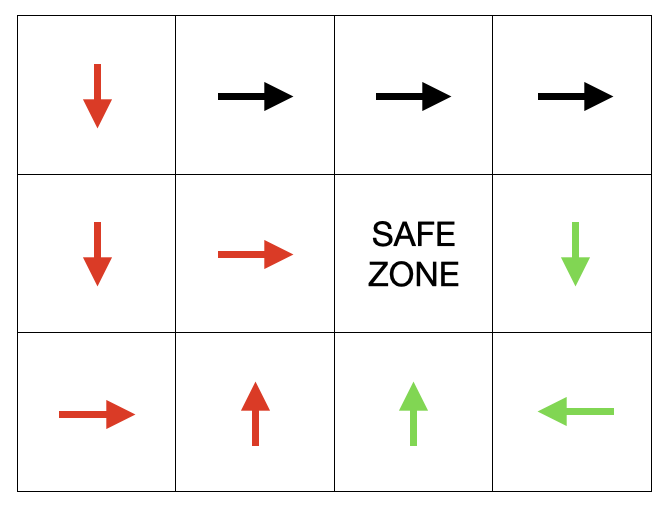
3. 집합의 개수가 곧 SAFE ZONE의 개수이다.
SAFE ZONE을 공유하는 칸들을 하나의 집합으로 묶은 것이기 때문에, 집합의 개수가 곧 SAFE ZONE의 개수가 된다.
import Foundation
var N = 0, M = 0
var map = Array(repeating: [Character](), count: 1001)
var parent = Array(repeating: Array(repeating: Pair(0,0), count: 1001), count: 1001)
var rank = Array(repeating: Array(repeating: 0, count: 1001), count: 1001)
var visit = Array(repeating: Array(repeating: false, count: 1001), count: 1001)
struct Pair: Hashable {
let row: Int
let col: Int
init(_ row: Int, _ col: Int) {
self.row = row
self.col = col
}
}
func find(_ p: Pair) -> Pair {
if parent[p.row][p.col] == p { return p }
parent[p.row][p.col] = find(parent[p.row][p.col])
return parent[p.row][p.col]
}
func union(_ p1: Pair, _ p2: Pair) {
var parentP1 = find(p1), parentP2 = find(p2)
if parentP1 == parentP2 { return }
if rank[parentP1.row][parentP1.col] < rank[parentP2.row][parentP2.col] {
swap(&parentP1, &parentP2)
}
parent[parentP2.row][parentP2.col] = parentP1
rank[parentP1.row][parentP1.col] += rank[parentP2.row][parentP2.col]
}
func DFS(_ p: Pair) {
visit[p.row][p.col] = true
let dr: Int, dc: Int
switch map[p.row][p.col] {
case "U":
dr = -1; dc = 0
case "D":
dr = 1; dc = 0
case "R":
dr = 0; dc = 1
case "L":
dr = 0; dc = -1
default:
dr = 0; dc = 0
}
let adjacent = Pair(p.row + dr, p.col + dc)
guard (0..<N) ~= adjacent.row && (0..<M) ~= adjacent.col else { return }
union(p, adjacent)
if !visit[adjacent.row][adjacent.col] { DFS(adjacent) }
}
func initParent() {
for i in 0..<N {
for j in 0..<M {
parent[i][j] = Pair(i, j)
}
}
}
func solution() {
let input = readLine()!.split(separator: " ").map{ Int(String($0))! }
N = input[0]
M = input[1]
initParent()
for i in 0..<N { map[i] = readLine()!.map{ $0 } }
for i in 0..<N {
for j in 0..<M {
if !visit[i][j] { DFS(Pair(i, j)) }
}
}
var set = Set<Pair>()
for i in 0..<N {
for j in 0..<M {
set.insert(find(Pair(i, j)))
}
}
print(set.count)
}
solution()
'Problem Solving > BOJ' 카테고리의 다른 글
| 백준 17143번 낚시왕 - 스위프트(Swift) 풀이 + 그림 설명 (0) | 2022.02.05 |
|---|---|
| 백준 16946번 벽 부수고 이동하기 4 - 스위프트(Swift) 풀이 + 그림 설명 (0) | 2022.02.05 |
| 백준 1766번 문제집 - C++(cpp) 풀이 (0) | 2022.02.04 |
| 백준 1007번 백터 매칭 - 스위프트(Swift) 풀이 (0) | 2022.02.04 |
| 백준 2342번 Dance Dance Revolution - 스위프트(Swift) 풀이 (0) | 2022.02.03 |




댓글