반응형
1. 첫 번째 수부터 i번째 수 까지의 합을 저장하는 누적합 배열을 만든다. psum[i] = arr[0] + arr[1] + arr[2] + ... + arr[i]
2. arr[i] ~ arr[j] 의 구간 합은 psum[j] - psum[i - 1]과 같다.
3. i = 0인 경우 예외 처리를 해준다.
1. 첫 번째 수부터 i번째 수 까지의 합을 저장하는 누적합 배열을 만든다. psum[i] = arr[0] + arr[1] + arr[2] + ... + arr[i]
구간 i부터 j까지 반복문을 돌면서 실제로 돌면 M개의 쿼리에 대해 O(N)이 걸리는 작업을 수행하므로 총 O(NM)의 시간 복잡도를 갖는다. 이 방법으로는 N과 M이 각각 최대 10^5이므로 시간초과가 날 것이다.
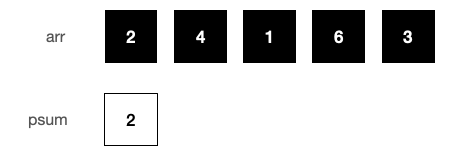
구간합을 O(1)에 구할 수 있는 방법이 있다. 일단 누적합(Prefix Sum) 배열을 만든다. 누적합 배열은 O(N)에 만들 수 있다.
psum[i] = psum[i-1] + arr[i]
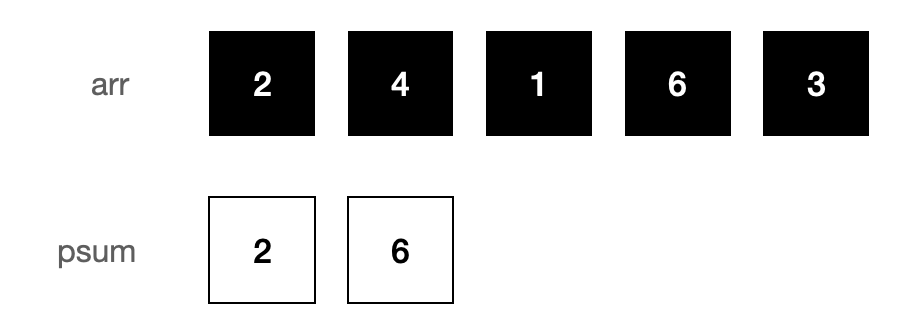

2. arr[i] ~ arr[j] 의 구간 합은 psum[j] - psum[i - 1]과 같다.

arr[2] ~ arr[4]의 구간합은 (arr[0] ~ arr[4]의 합) - (arr[0] ~ arr[1]의 합)과 같다.
arr[0] ~ arr[4]의 합은 psum[4]이고,
arr[0] ~ arr[1]의 합은 psum[1]이므로
psum[4] - psum[1]로 구할 수 있다.
이를 일반화하면, arr[i] ~ arr[j] 의 구간 합은 psum[j] - psum[i - 1]과 같다.
3. i = 0인 경우 예외 처리를 해준다.
i = 0인 경우 psum[i-1]이 psum[-1]이 되므로 Index out of range 에러가 난다. 따라서 i = 0일 경우에만 psum[i - 1]은 0으로 대신해준다.
import Foundation
func solution() -> String {
var input = readLine()!.split(separator: " ").map{ Int(String($0))! }
let N = input[0]
let M = input[1]
let arr = readLine()!.split(separator: " ").map{ Int64(String($0))! }
var psum = Array(repeating: arr[0], count: N)
for i in 1..<N {
psum[i] = psum[i-1] + arr[i]
}
var result = ""
for _ in 0..<M {
input = readLine()!.split(separator: " ").map{ Int(String($0))! }
let lo = input[0] - 1
let hi = input[1] - 1
let sumFromLoToHi = psum[hi] - (lo == 0 ? 0 : psum[lo - 1])
result.write("\(sumFromLoToHi)\n")
}
return result
}
print(solution())
반응형
'Problem Solving > BOJ' 카테고리의 다른 글
| 백준 9019번 DSLR - 스위프트(Swift) 시간초과 해결 (0) | 2022.01.21 |
|---|---|
| 백준 6064번 카잉 달력 - 스위프트(Swift) 풀이 + 그림 설명 (0) | 2022.01.21 |
| 백준 7569번 토마토 - 스위프트(Swift) 풀이 + 그림 설명 (0) | 2022.01.18 |
| 백준 10026번 적록색약 - 스위프트(Swift) 풀이 (0) | 2022.01.18 |
| 백준 5430번 AC - 스위프트(Swift) 풀이 + 그림 설명 (0) | 2022.01.18 |




댓글