아이디어가 생각이 안 나서 결국 검색으로 해결한 문제ㅠㅠ DP라는 것은 감이 왔는데 지금까지 풀었던 DP 방식은 시간 초과 때문에 적용할 수가 없었다. 처음에 떠올렸던 방식은 dp(count, index, targetWeight) = weights[index...] 에서 count개의 소포를 뽑아 targetWeight를 딱 맞출 수 있는지 여부로 두고, index번째 item을 뽑는 경우 & 뽑지 않는 경우를 모두 고려하여 아래와 같은 식으로 푸는 것이었다. 하지만 count는 4, index는 5000, targetWeight는 무려 799,994여서 4*5000*799,994로 시간 안에 풀어낼 수가 없다..
dp(count, index, targetWeight)
= dp(count - 1, index + 1, targetWeight - weights[index]) OR dp(count, index + 1, targetWeight)
정말 모르겠어서 검색으로 아이디어를 얻었다. 포인트는 4개를 2개 + 2개로 나눠서 뽑는 것이다!! 일단 n개를 인덱스 i를 기준으로 반으로 가른다. 그리고 왼쪽 더미에서 2개, 오른쪽 더미에서 2개를 뽑아 무게를 w로 만들 수 있는지 체크하는 것이다.

먼저 2중 for문을 돌면서 오른쪽 더미에서 나머지 소포 하나 j를 뽑는다. 이제 왼쪽 더미에서도 2개를 뽑아야 하는데, 또 for문을 돌아서 두 개를 뽑으면 4중 for문이 돼서 당연히 시간 초과가 나게 된다. 그럼 어떻게 해야 할까? 바로 여기서 dp를 사용하면 된다! (이것도 dp겠지..?)

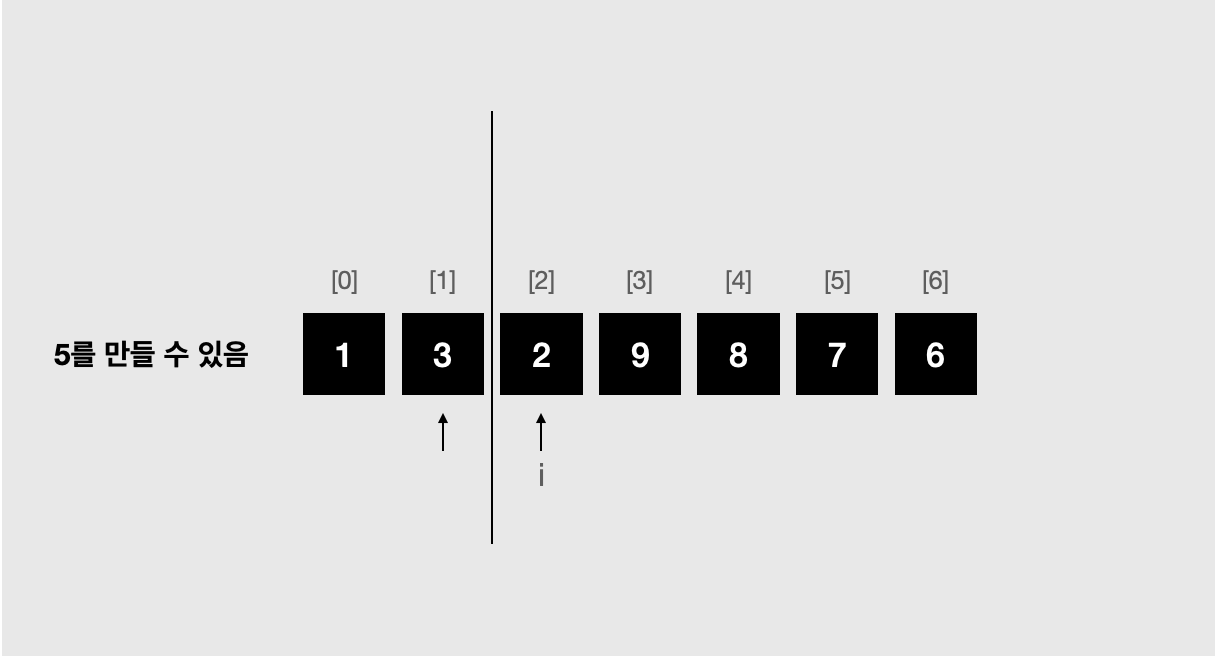
왼쪽 더미에서는 구체적으로 두 개를 뽑는 대신, 두 개를 뽑아서 원하는 무게를 만들 수 있는지 여부만 확인해주면 된다. 아래 그림과 같은 상황으로 예를 들면, 현재 오른쪽 더미에서 9와 7을 뽑아 무게 합이 16인 상태이다. 만약 w가 20이라면, 20-16=4이므로 왼쪽 더미에서 2개를 뽑아 4를 만들 수 있으면 된다. 기록해둔 것을 보면 4는 만들 수 있으므로 가능한 경우를 찾았고, 따라서 반복문을 멈춰도 된다. 그럼 도대체 어떻게 진짜로 뽑지 않고도 원하는 무게를 만들 수 있는지 여부를 알까?

이전 i들을 돌 때 미리 뽑아서 기록해두면 된다! i를 기준으로 반으로 가르는 경우는 총 n가지가 있으므로 i를 0부터 n-1까지 하나씩 오른쪽으로 옮기면서 모든 경우를 탐색해줘야 할 것이다. 현재 i=3인데 하나 전으로 돌아가서 i=2인 상황으로 가보자. weights[0... 1]에서 하나, 그리고 현재 i인 weights[2] 이렇게 총 두 개를 뽑았을 때 만들 수 있는 무게를 미래를 위해 기록해두자. 더 전인 i=1일 때도 weights[0]과 weights[1]을 뽑았을 때 만들 수 있는 무게를 기록해둔다. i-1일 때는 (i-1, [0...i-2]에서 한 개)를 뽑는 모든 경우를 고려해두고, i-2일 때는 (i-2, [0...i-1]에서 한 개)를 뽑는 모든 경우를 고려해두고.. 즉, 미래를 위해 과거에 미리 2중 for문을 돌아둔 것이 된다.

따라서 i를 고정하고 나서 j를 [j+1...]까지 한 번, 그리고 미래를 위해 [0...i-1]까지 또 한 번 반복문을 돌려주어야 한다. 따라서 시간 복잡도는 O(n^2)이 된다. n이 5,000이므로 충분히 풀 수 있다.
for i in 0..<n-1 {
for j in i+1..<n { } // 우측 더미에서 한 개 마저 뽑기
for j in 0..<i { } // 미래를 위해 i와 [0...i-1]에서 한 개 뽑기를 미리 해둠
}
'Problem Solving > BOJ' 카테고리의 다른 글
| 백준 15824번 너 봄에는 캡사이신이 맛있단다 - 스위프트(Swift) 풀이 (0) | 2022.01.09 |
|---|---|
| 백준 3015번 오아시스 재결합 - 스위프트(Swift) 풀이 + 그림 설명 (0) | 2022.01.08 |
| 백준 14725번 개미굴 - 스위프트(Swift) 풀이 + 그림 설명 (0) | 2022.01.06 |
| 백준 2533번 사회망 서비스(SNS) - C++(cpp) 풀이 (0) | 2022.01.06 |
| 백준 2533번 사회망 서비스(SNS) - 스위프트(Swift) 시간초과 해결 (0) | 2022.01.06 |




댓글