반응형
1. 세 개 이상의 연결선이 한 점에서 만나지 않으므로, 교차하는 선분 쌍의 개수가 곧 교차점의 개수이다.
2. 한 선분이 다른 선분을 완전히 포함하는 경우에는, 교차하지 않는 것으로 판정한다.
3. 모든 선분 쌍에 대해 교차 여부를 구하면서 총 교차점 수와 최대 교차점 수를 구한다.
1. 세 개 이상의 연결선이 한 점에서 만나지 않으므로, 교차하는 선분 쌍의 개수가 곧 교차점의 개수이다.
두 점을 직선으로만 잇는다면 세 개의 선분 A, B, C가 한 점에서 만날 수 있다. 이때 선분 쌍 AB, BC, 그리고 CA가 교차한다. 그런데 세 개 이상의 선분을 한 점에서 만나도록 하면 안 된다. 즉 각 선분 쌍이 모두 다른 점에서 만나도록 해야 하므로, 선분 쌍의 개수가 곧 교차점의 개수와 같게 된다.
2. 한 선분이 다른 선분을 완전히 포함하는 경우에는, 교차하지 않는 것으로 판정한다.
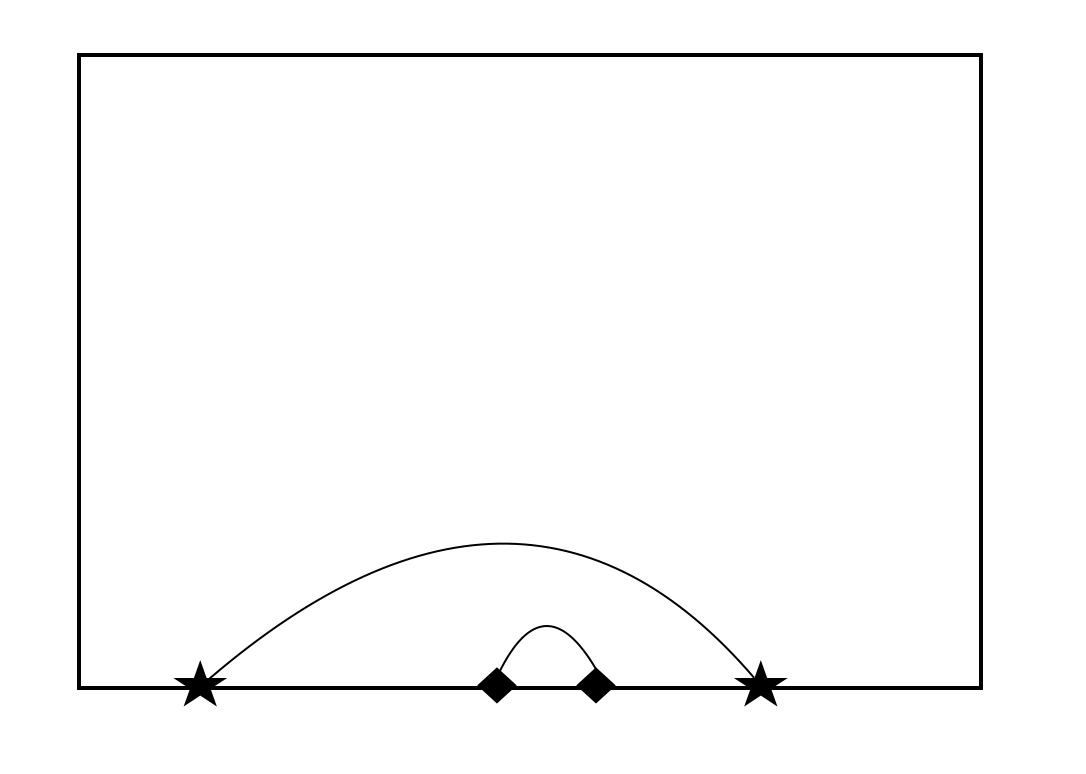
교차점의 개수를 최소화해야 한다. 곡선으로 잇는 것이 가능하기 때문에 아래와 같은 경우는 예외처리가 필요하다. 한 선분이 다른 선분을 완전히 포함하는 경우에는 아래처럼 잇는다면 교차하지 않도록 할 수 있다. 따라서 이 경우에는 일반적인 선분 교차와 다르게 교차하지 않는 것으로 판정해야 한다.
3. 모든 선분 쌍에 대해 교차 여부를 구하면서 총 교차점 수와 최대 교차점 수를 구한다.
모든 선분 쌍에 대해 교차 여부를 구해서 총 교차점의 수와 최대 교차점을 갖는 선분을 구하면 된다. 모든 선분 쌍을 탐색하므로 시간복잡도는 O(N^2)이 된다. 선분 교차 여부는 CCW를 이용하여 구했다. (점의 위치가 직사각형의 변 위로 한정되기 때문에 CCW를 사용하지 않고도 풀이가 가능한데 가장 먼저 떠오른 것이 CCW라 이를 활용해서 풀이해보았다.)
반응형
#include <iostream>
using namespace std;
typedef long long ll;
struct Point {
ll x, y;
Point() { x=0; y=0; }
Point(ll X, ll Y) : x(X), y(Y) {}
Point operator - (Point &other) {
return Point(other.x - x, other.y - y);
}
ll operator * (Point &other) {
return x * other.y - y * other.x;
}
bool operator <= (Point &other) {
if (x == other.x) return y <= other.y;
else return x <= other.x;
}
};
struct LineSegment {
Point p1, p2;
LineSegment() { p1=Point(); p2 = Point(); }
LineSegment(Point P1, Point P2) : p1(P1), p2(P2) {}
};
int N;
LineSegment segs[50];
ll ccw(Point p1, Point p2, Point p3) {
Point v1 = p2 - p1;
Point v2 = p3 - p2;
ll p = v1 * v2;
if (p > 0) return 1;
else if (p < 0) return -1;
else return 0;
}
bool check_intersect(LineSegment s1, LineSegment s2) {
Point p1 = s1.p1, p2 = s1.p2, p3 = s2.p1, p4 = s2.p2;
ll ccw1 = ccw(p1, p2, p3);
ll ccw2 = ccw(p1, p2, p4);
ll ccw3 = ccw(p3, p4, p1);
ll ccw4 = ccw(p3, p4, p2);
ll result1 = ccw1 * ccw2;
ll result2 = ccw3 * ccw4;
if (result1 > 0 || result2 > 0) return false;
else if (result1 == 0 && result2 == 0) {
if (p2 <= p1) swap(p1, p2);
if (p4 <= p3) swap(p3, p4);
if (p3 <= p1) {
swap(p1, p3);
swap(p2, p4);
}
if (p1 <= p4 && p3 <= p2) {
// 포함되는 경우에는 교차하지 않도록 할 수 있음
if (p4 <= p2) return false;
else return true;
}
else return false;
}
else return true;
}
Point to_point(ll t, ll d) {
switch (t) {
case 1:
return Point(d, 51);
case 2:
return Point(d, 0);
case 3:
return Point(0, 51-d);
case 4:
return Point(51, 51-d);
default:
return Point(0, 0);
}
}
pair<ll, ll> count_intersect() {
ll total_cnt = 0, max_cnt = 0;
// 세 개 이상의 연결선이 한 점에서 만나지 않으므로 교차 쌍만큼 교차점이 생김.
// 교차쌍의 개수 = 교차점의 개수
for (int i=0; i<N; i++) {
ll cnt = 0;
for (int j=0; j<N; j++) {
if (i == j) continue;
if (check_intersect(segs[i], segs[j])) cnt++;
}
max_cnt = max(max_cnt, cnt);
total_cnt += cnt;
}
total_cnt /= 2;
return {total_cnt, max_cnt};
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
cin >> N; N /= 2;
for (int i=0; i<N; i++) {
ll t1, d1, t2, d2;
cin >> t1 >> d1 >> t2 >> d2;
segs[i] = LineSegment(to_point(t1, d1), to_point(t2, d2));
}
pair<ll, ll> ans = count_intersect();
cout << ans.first << "\n" << ans.second << "\n";
return 0;
}
반응형
'Problem Solving > BOJ' 카테고리의 다른 글
| 백준 5175번 문제없는 문제 - C++(cpp) 풀이 (0) | 2022.04.11 |
|---|---|
| 백준 13398번 연속합 2 - C++(cpp) 풀이 (0) | 2022.04.08 |
| 백준 5557번 1학년 - C++(cpp) 풀이 (0) | 2022.04.06 |
| 백준 1405번 미친 로봇 - C++(cpp) 풀이 (0) | 2022.04.05 |
| 백준 1041번 주사위 - C++(cpp) 풀이 (0) | 2022.04.04 |




댓글